![]()
室温イオン液体は、NaClに代表される溶融塩とは異なり、室温でも融解している。それは、嵩高い有機イオンで構成されているので、異種イオン間のクーロン引力が小さいためである考えられている。さらに面白いことには、正電荷が陽イオンの一部に局在しているため、その正電荷部分と陰イオンが引き合って極性のドメイン構造を形成し、一方、陽イオンの残りの中性部分(鎖状構造を有する場合が多い)は束になって非極性のドメインを形成している。しかし、このようなドメイン構造がダイナミクスにどのように反映されるのか、未解明であった。また、ドメイン構造がメゾスケールの不均一性であるのに対し、液体表面の形成はマクロスケールでの不均一性であり、この両者がどのような関係にあるのかも、興味深い問題である。以下では、 (1)ドメイン構造のダイナミクス、(2)メゾ不均一性とマクロ不均一性の関係、さらには(2)の研究を通して得られた副産物である(3)表面張力波の分散関係について解説する。これらはいずれも、不規則系研究室の最近の研究成果である。
極性ドメインではクーロン力が支配的なので機械的性質は「剛」であるが、非極性ドメインではファン・デル・ワールス力が働いているので「柔」である。我々は、室温イオン液体に音圧を加えると、非常に面白い粘弾性挙動を示すことを発見している。粘弾性の研究は、ソフトマター分野では頻繁に行われているが、微視的相互作用との関連において研究した例は少ない。
我々は、典型的な室温イオン液体(具体的には、[C4mim][PF6]、[C6mim][PF6]、
[C8mim][PF6]、[C4mim][TFSA]などと略称されているもの)について、超音波吸収の3周波数同時測定を、室温から140℃程度の温度まで系統的に行った。その結果、通常のNewton液体では説明できない著しい周波数依存性を見出した。実験データを、3次元双連結ソフトマターに対して最近提案された理論に従い、Maxwell型の緩和を仮定して解析した結果、
①Maxwellモデルの剛性Gは陰イオン種に大きく依存するがアルキル鎖長には殆ど依存しないこと[図1左参照]、一方、②緩和時間τは逆にアルキル鎖長に強く依存すること[図1右参照]が見出された。即ち、双連結ドメイン構造を仮定すれば、特異なダイナミクスも説明されることが分かった。さらに、Maxwellモデルの範囲内で、吸収の周波数依存性から音速を見積もることにより、少なくとも室温、低周波域においては、京大・化学・木村先生グループが報告されている著しい音波分散を再現することも確認している。
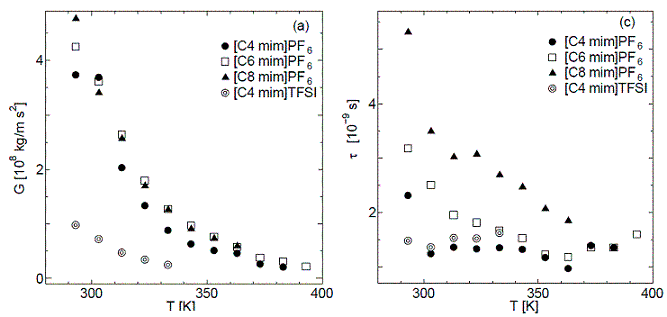 |
| [図1]粘弾性パラメータ(Maxwellモデル)の温度依存性 |
室温イオン液体(RTIL)は、新しい化学反応場として注目されており、誘電的性質は、その溶解度の支配因子である。
しかし、従来の研究には実験技術上、学術上、双方において大きな問題を抱えていた。
前者については、反射法マイクロ波分光を用いていたので、参照試料やプローブ周縁の電場補正が必要であったため、実験データの信頼性そのものに問題があった。
後者については、極性・非極性ドメインの存在と、均一液体を仮定して導出される誘電率との整合性について、手つかずの状態であった。
我々は、この二つの問題を一挙に解決した。
まず測定法として、参照試料や周縁電場補正が要らない透過法を採用した(図2)。
白金管を外導体、白金線を内導体、石英を誘電体に利用したもので、2本の石英棒の隙間に試料液体を導入する。
これをRTILに適用して誘電率を求めるために、直流伝導度の効果を適正に取り込む新しい解析法を開発した。
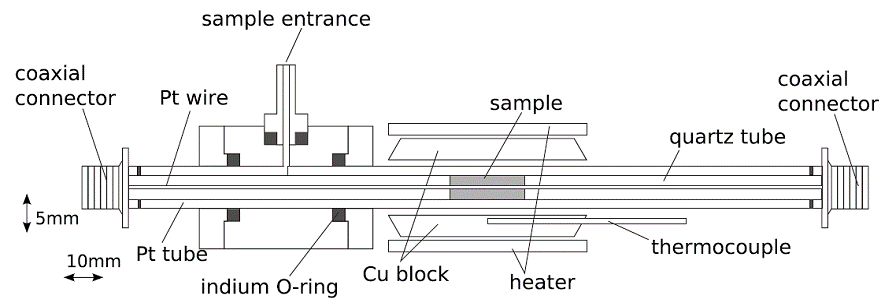 |
| [図2]透過法測定の模式図 |
図3に、イミダゾリウムのTFSA塩とPF6塩の静的誘電率の温度依存性を示す。 我々のデータ(closed
symbols)は高温まで安定して測定されている。顕著な特徴は、アルキル鎖が長くなると誘電率が系統的に小さくなることである。
これに着目して、非極性ドメインの局所誘電率ε npはアルキル鎖長に依存しないと仮定して、有効媒質近似の下、εnpと極性ドメインの誘電率εpとの関係を示したのが図4である。
アニオンを共通とする3つの試料の関係式が共通の交点をもつことから、εnp=2.5、εp
=20と極めて合理的な値が得られた。 即ち、RTILが不均一な化学反応場を提供することが実験的にも証明された。
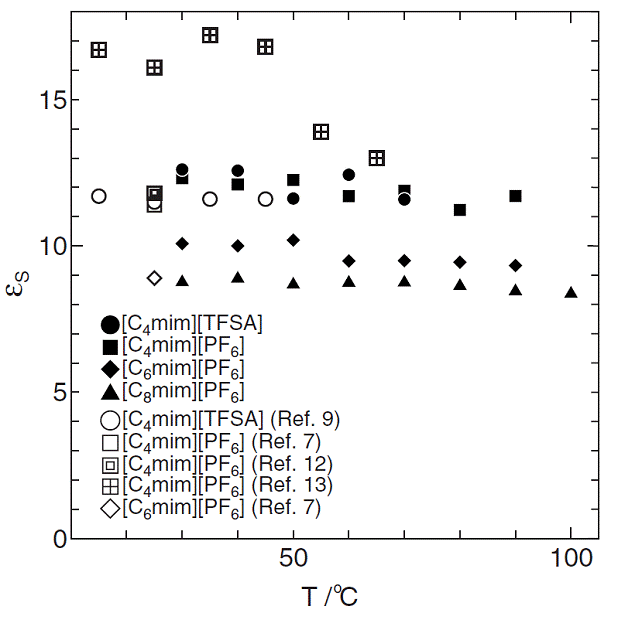 |
| [図3]イミダゾリウムのTFSA塩とPF6塩の静的誘電率の温度依存性 |
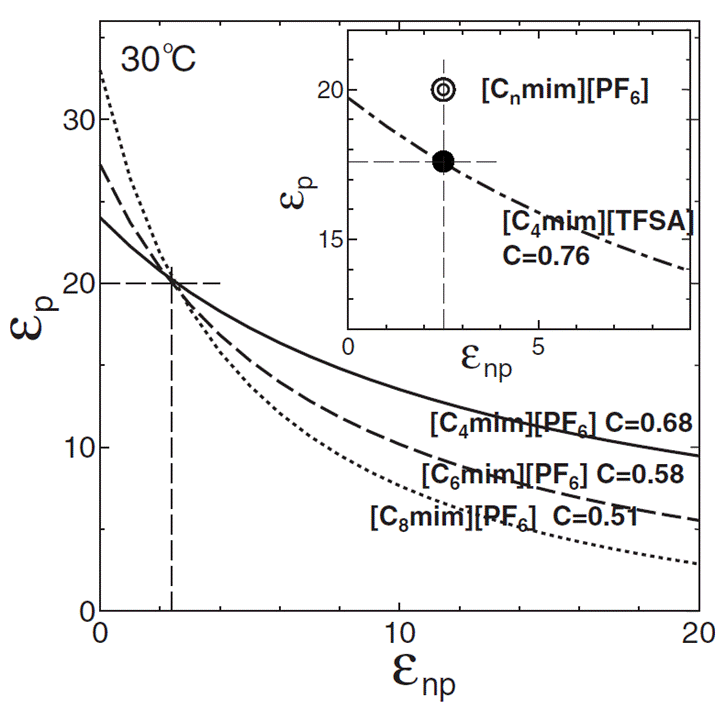 |
| [図4]非極性ドメインの局所誘電率εnpと極性ドメインの誘電率εpとの関係 |
表面反射型の動的光散乱装置を自作で立ち上げ、室温イオン液体の表面張力波のパワースペクトルの観測を行い、流体力学と揺動散逸定理から導かれる厳密な表式を用いて解析した結果、粘性および表面張力が正しく与えられることが分かった。しかも、この方法は非接触法であるので、伝統的な粘性・表面張力測定より、高い温度域まで適用可能であるため、例えば表面張力の温度微分として与えられる表面過剰エントロピーも正確に求められることが判明した。陰イオンのサイズやアルキル側鎖長を系統的に変えて測定した結果、陰イオンサイズの減少(即ち、クーロン引力の増大)に伴って粘性、表面張力の双方が増加するが、アルキル側鎖長増大の場合には、良く知られているように粘性は増大するが、表面張力は逆に減少することを確認した。この結果は、メゾ不均一性とマクロ不均一性の成因が異なること、クーロン相互作用のみでは説明できないことを示唆している。参考のため、イオン性の度合いを表す有効イオン濃度 Ceffと、van der Waals力の度合いを表すとして我々が導入した側鎖上の炭素数の平面上に、種々の室温イオン液体の粘性と表面張力の値を書き込んだものを図5に示す。 (a)図の実線は、粘性が50mPa sの等高線に対応し、(b)図の実線は、表面張力が33.8mN/mに対応する。さらに、表面エントロピーが正であり、(表面張力ではなく)粘性と同じ物質依存性をもつことから、表面ではドメイン構造が緩和していると結論される。また、表面張力のアルキル鎖長依存性に加えて、表面張力の絶対値がNaClなど従来からのイオン性液体に比べて小さく、、むしろ分子性液体に近いことなどの実験結果は、光学測定から提唱されている「アルキル鎖が表面垂直に配列している描像」と整合している。
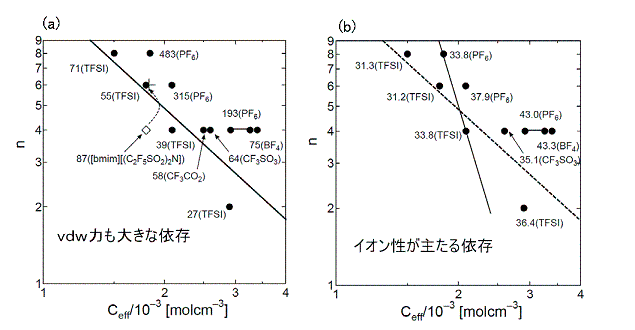 |
| [図5]有効イオン濃度Ceffと側鎖上の炭素数nの平面上に、種々のイオン液体の粘性(a)と表面張力(b)を示す。 |
表面張力波の分散関係は、理論的には線形化Navier-Stokes方程式と揺動散逸定理の組み合わせで定式化されており、低波数極限では減衰振動する進行波であるが高波数極限では過減衰して伝播しなくなること、両者の中間波数領域では進行波から過減衰への転移が起こることが知られている。しかし、その全貌を捉えた実験的は行われていなかった。我々は、室温付近で粘性が著しく変化するイオン液体を試料として取り上げることにより、①温度または波長の変化に伴う振動・過減衰転移の系統的発見、②転移点近傍での速い緩和モードも含めた表面波分散関係の全体像観察を行っている。特に、②については、全ての液体を通して初めての成果である。
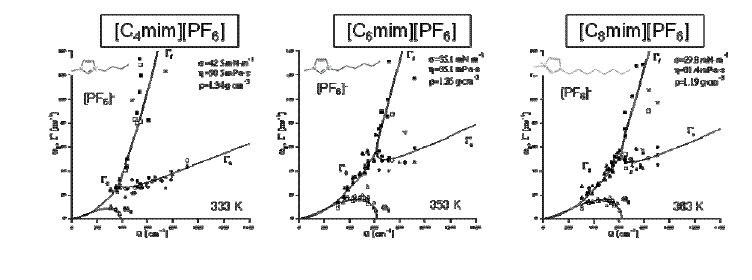 |
| [図6]表面張力波の分散関係。時間領域(記号)と周波数領域(実線)の解析はよく一致している。 |